Projective blue-noise sampling

Computer Graphics Forum, 2015 (presented at EGSR 2016)

Our projective blue-noise distributions (a, bottom) have blue-noise spectra in 2D as well as in their 1D projections, while classic 2D blue noise (a, top) has an almost white-noise spectrum in 1D. Applications include Monte Carlo rendering (b), reconstruction (c), as well as placement of primitives (d) such that they are well-distributed both in 3D and when projected to 2D.

Abstract

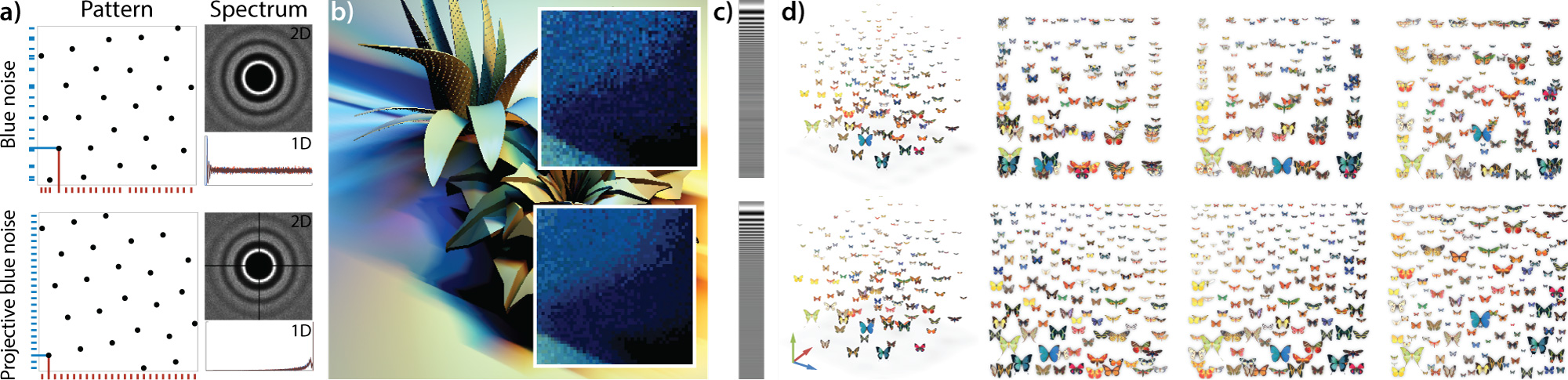
We propose projective blue-noise patterns that retain their blue-noise characteristics when undergoing one or multiple projections onto lower-dimensional subspaces. These patterns are produced by extending existing methods, such as dart throwing and Lloyd relaxation, and have a range of applications. For numerical integration, our patterns often outperform state-of-the-art stochastic and low-discrepancy patterns, which have been specifically designed only for this purpose. For image reconstruction, our method outperforms traditional blue-noise sampling when the variation in the signal is concentrated along one dimension. Finally, we use our patterns to distribute primitives uniformly in 3D space such that their 2D projections retain a blue-noise distribution.

Downloads and links

  • paper (PDF, 7.5 MB)
  • citation (BIB)
  • slides – from the conference presentation (PPTX, 123 MB)
  • video – YouTube
  • image comparison – an interactive JavaScript comparison of our 2D patterns against prior state-of-the-art methods

Media

Video

BibTeX reference

@article{Reinert:2015:ProjectiveBlueNoise,
  author = {Bernhard Reinert and Tobias Ritschel and Hans-Peter Seidel and Iliyan Georgiev},
  title = {Projective Blue-Noise Sampling},
  journal = {Computer Graphics Forum},
  year = {2015},
  issn = {1467-8659},
  keywords = {sampling, blue-noise, monte carlo rendering, image reconstruction, primitive placement}
}