Automatic Sampling for Discontinuities in Differentiable Shaders
Abstract
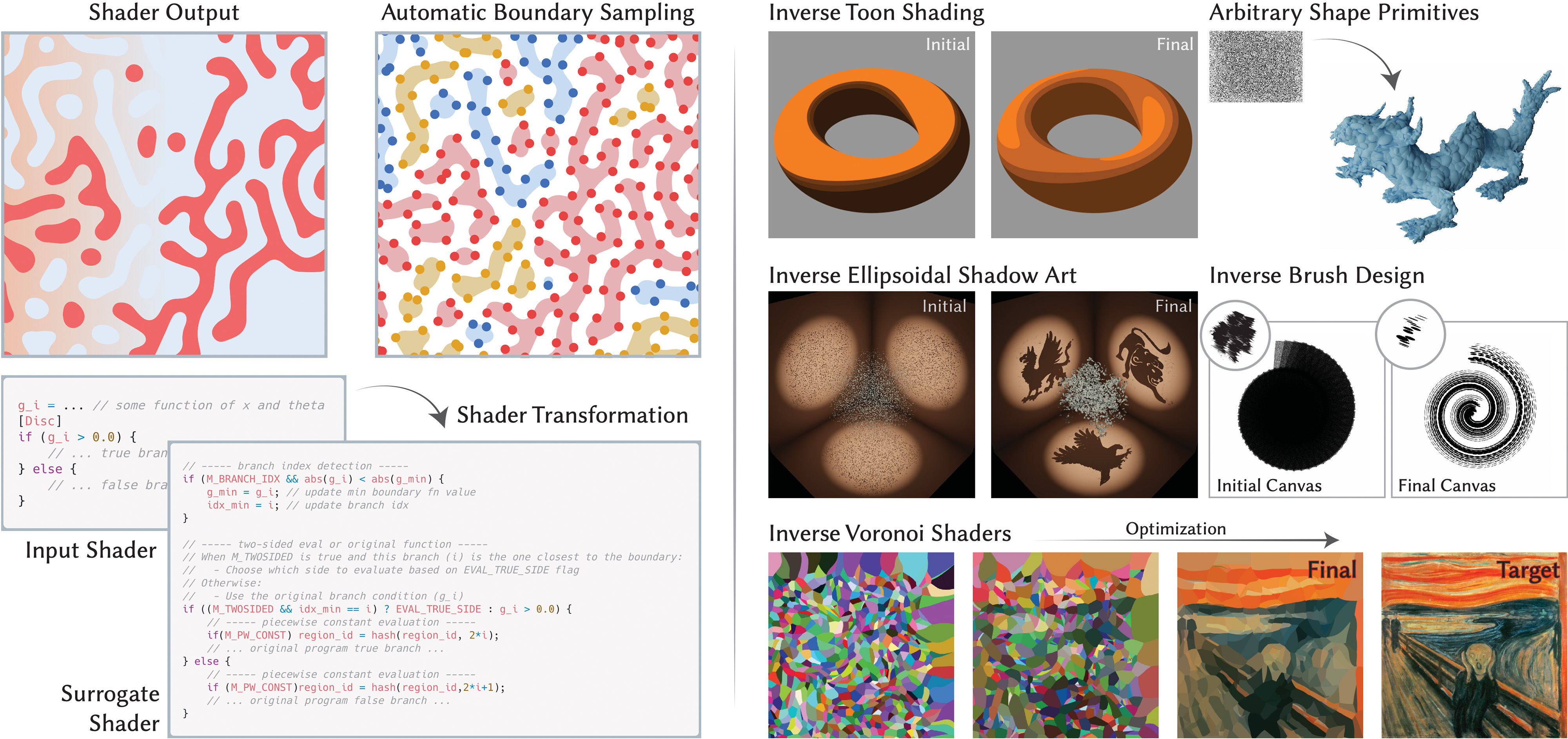
We present a novel method to differentiate integrals of discontinuous functions, which are common in inverse graphics, computer vision, and machine learning applications. Previous methods either require specialized routines to sample the discontinuous boundaries of predetermined primitives, or use reparameterization techniques that suffer from high variance. In contrast, our method handles general discontinuous functions, expressed as shader programs, without requiring manually specified boundary sampling routines. We achieve this through a program transformation that converts discontinuous functions into piecewise constant ones, enabling efficient boundary sampling through a novel segment snapping technique, and accurate derivatives at the boundary by simply comparing values on both sides of the discontinuity. Our method handles both explicit boundaries (polygons, ellipses, Bézier curves) and implicit ones (neural networks, noise-based functions, swept surfaces). We demonstrate that our system supports a wide range of applications, including painterly rendering, raster image fitting, constructive solid geometry, swept surfaces, mosaicing, and ray marching.
Downloads and links
BibTeX reference
@article{Belhe:2025:DiscontinuitySampling,
author = {Yash Belhe and Ishit Mehta and Wesley Chang and Iliyan Georgiev and Michaël Gharbi and Ravi Ramamoorthi and Tzu-Mao Li},
title = {Automatic sampling for discontinuities in differentiable shaders},
journal = {ACM Transactions on Graphics (Proceedings of SIGGRAPH Asia)},
year = {2025},
volume = {44},
number = {6},
doi = {10.1145/3763291}
}